发现需要上下文
当克里斯托弗·哥伦布和他的船员扬帆横渡大西洋时,他们并不是在寻找美洲。他们是在寻找一条通往印度的新航线,因为他们坚信地球是圆的。他们对新大陆一无所知,但既然他们是向西航行,他们就偶然发现了它。
他们无法达到他们的目标,因为地理条件不允许,但一旦他们意识到那不是印度,他们就宣布这是他们王室的“新发现”。如果我们认为水手需要水才能航行,那么我们就可以建立一个上下文,即在水上是积极的,在陆地上是消极的。一旦水手的搜索被陆地阻止,他们就无法再往前走,一条新的路线就找到了。让我们记住目标和上下文这两个概念,来探索 Qdrant 的新功能:发现搜索。
什么是发现搜索?
在 1.7 版本中,Qdrant 发布了这个新颖的 API,它允许您仅依靠纯向量来限制执行搜索的空间。这是一个强大的工具,可以让您以更受控的方式探索向量空间。它可用于查找不一定是离目标最近但仍与搜索相关的点。
您已经可以使用有效载荷过滤器来选择哪些点可用于搜索。这本身就非常灵活,因为它允许我们制作复杂的过滤器,以确定性地只显示满足其条件的点。然而,与每个点关联的有效载荷是任意的,无法告诉我们它们在向量空间中的位置。换句话说,过滤掉不相关的点可以看作是创建一个掩码而不是超平面——在正负向量之间切割——在空间中。
理解上下文
这就是向量上下文可以提供帮助的地方。我们将上下文定义为一个对列表。每对由一个正向量和一个负向量组成。通过上下文,我们可以在向量空间内定义超平面,这些超平面总是优先选择正向量而不是负向量。这有效地划分了执行搜索的空间。在空间被划分之后,我们 then 需要一个目标来返回与它更相似的点。
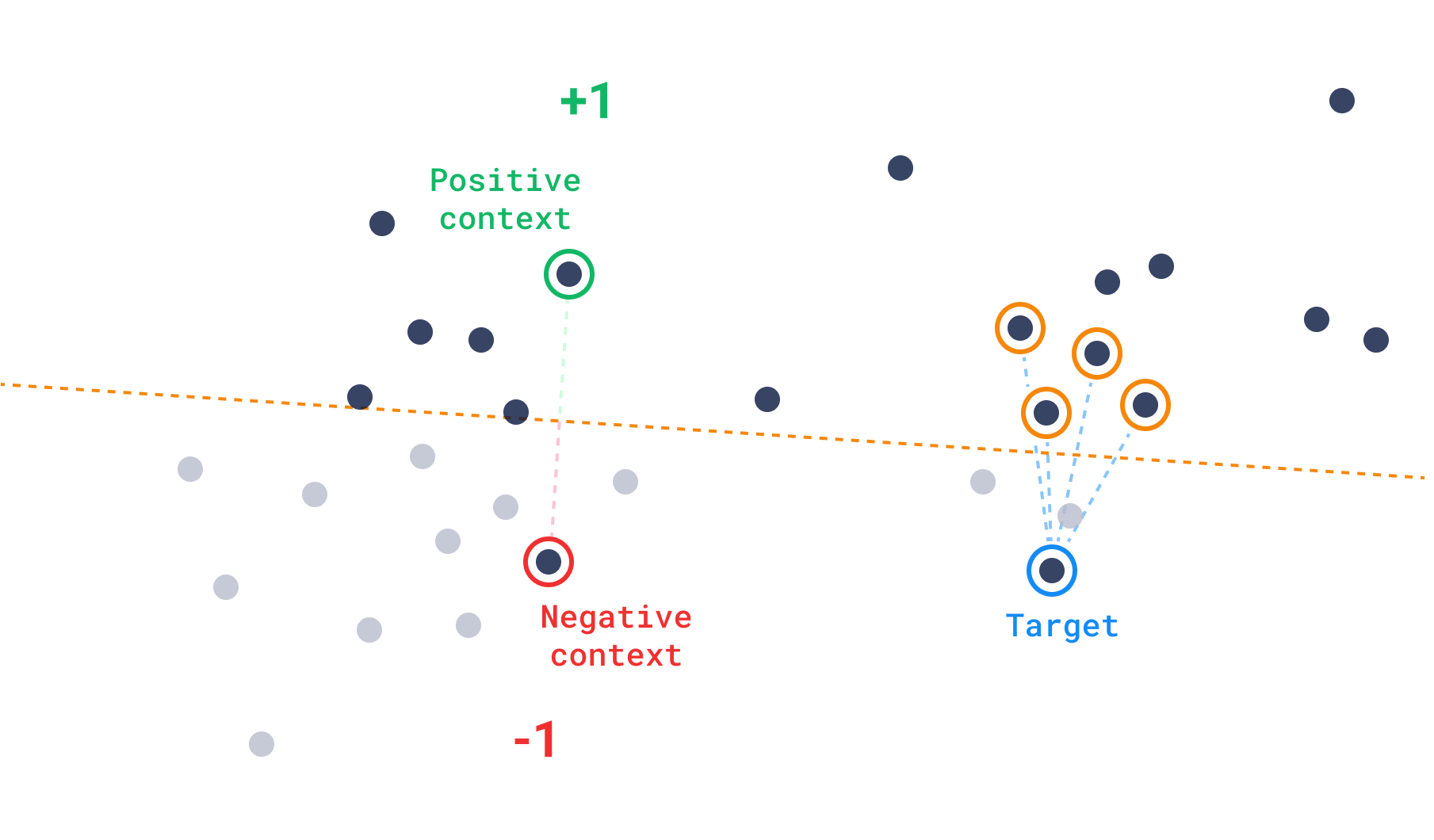
虽然正向量和负向量可能暗示使用推荐接口,但在上下文的情况下,它们需要以正负配对的方式出现。这受到机器学习概念三元组损失的启发,其中您有三个向量:一个锚点、一个正向量和一个负向量。三元组损失是对锚点与正向量相比更接近负向量的程度的评估,因此学习是通过“移动”正点和负点来尝试获得更好的评估。然而,在发现过程中,我们将正向量和负向量视为静态点,我们通过整个数据集搜索更符合此特征的“锚点”或结果候选点。
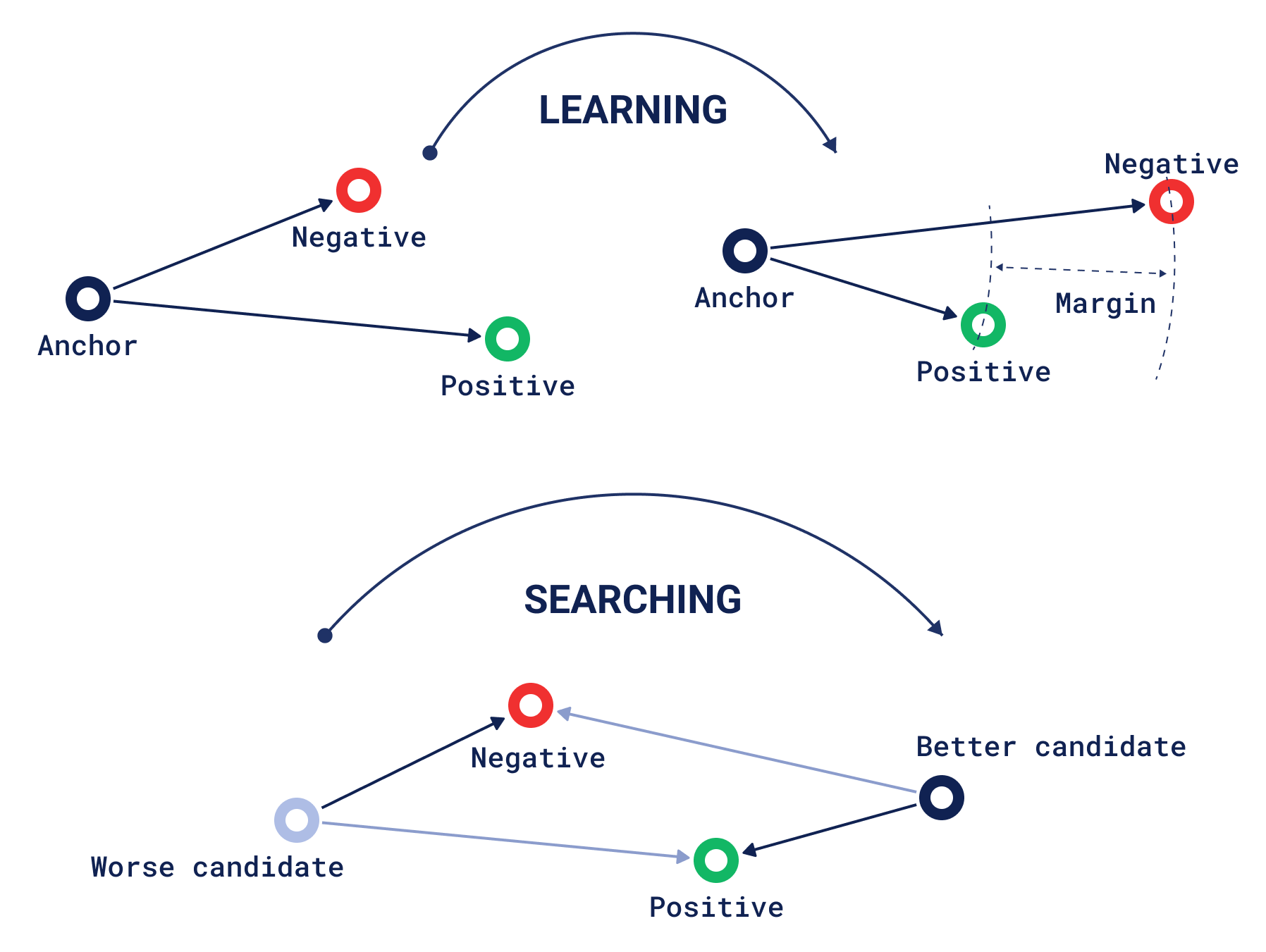
发现搜索因此由两个主要输入组成
- 目标:主要的兴趣点
- 上下文:我们刚刚定义的正点和负点对。
然而,这不是唯一的使用方式。或者,您可以只提供一个上下文,这会调用一个上下文搜索。当您想要探索由上下文定义的空间,但没有特定的目标时,这非常有用。但是请稍等,我们稍后会讲到这一点↪。
真实的发现搜索应用
让我们来谈谈第一种情况:带有目标的上下文。
要理解这为什么有用,让我们看一个真实的例子:使用多模态编码器(如 CLIP)通过文本和图像来搜索图像。CLIP 是一种神经网络,可以将图像和文本都嵌入到同一个向量空间中。这意味着您可以使用文本查询或图像查询来搜索图像。对于这个例子,我们将通过在文本输入中输入“burger”来重复使用我们的食物推荐演示。
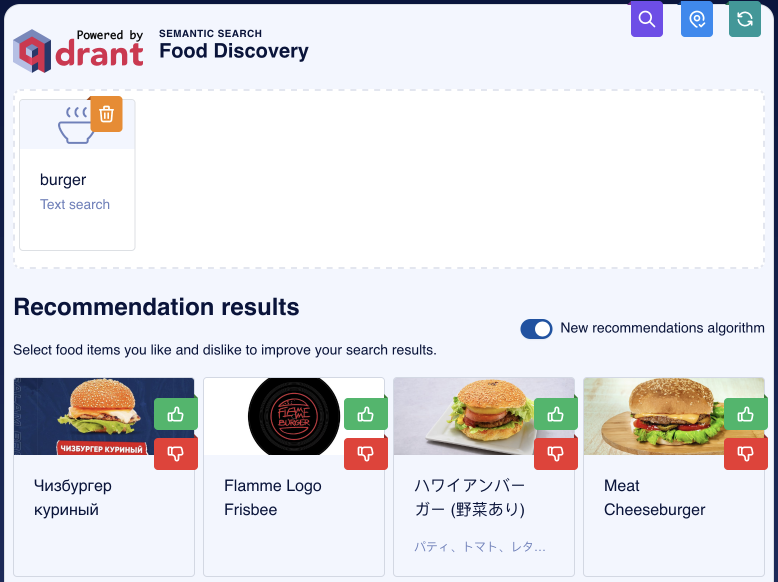
这基本上是最近邻搜索,虽然技术上我们只有汉堡的图像,但其中一张是汉堡的标志表示。不过,我们正在寻找真实的汉堡。让我们尝试通过将其添加为负例来排除像那样的图像。
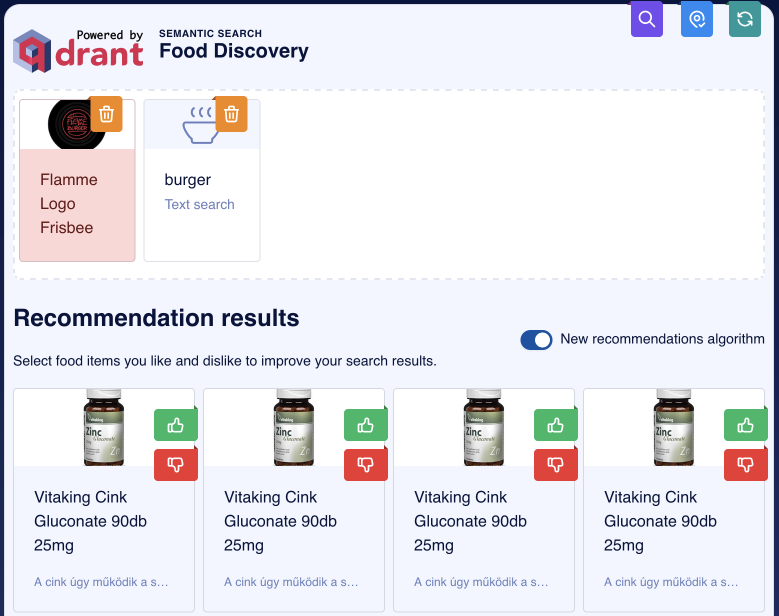
等等,刚才发生了什么?这些图片和汉堡完全无关,但它们仍然出现在前几个结果中。演示坏了吗?
事实证明,多模态编码器可能不会像你预期的那样工作。图像和文本嵌入在相同的空间中,但它们不一定彼此靠近。这意味着我们可以创建一个分布的心理模型,将其视为两个独立的平面,一个用于图像,一个用于文本。
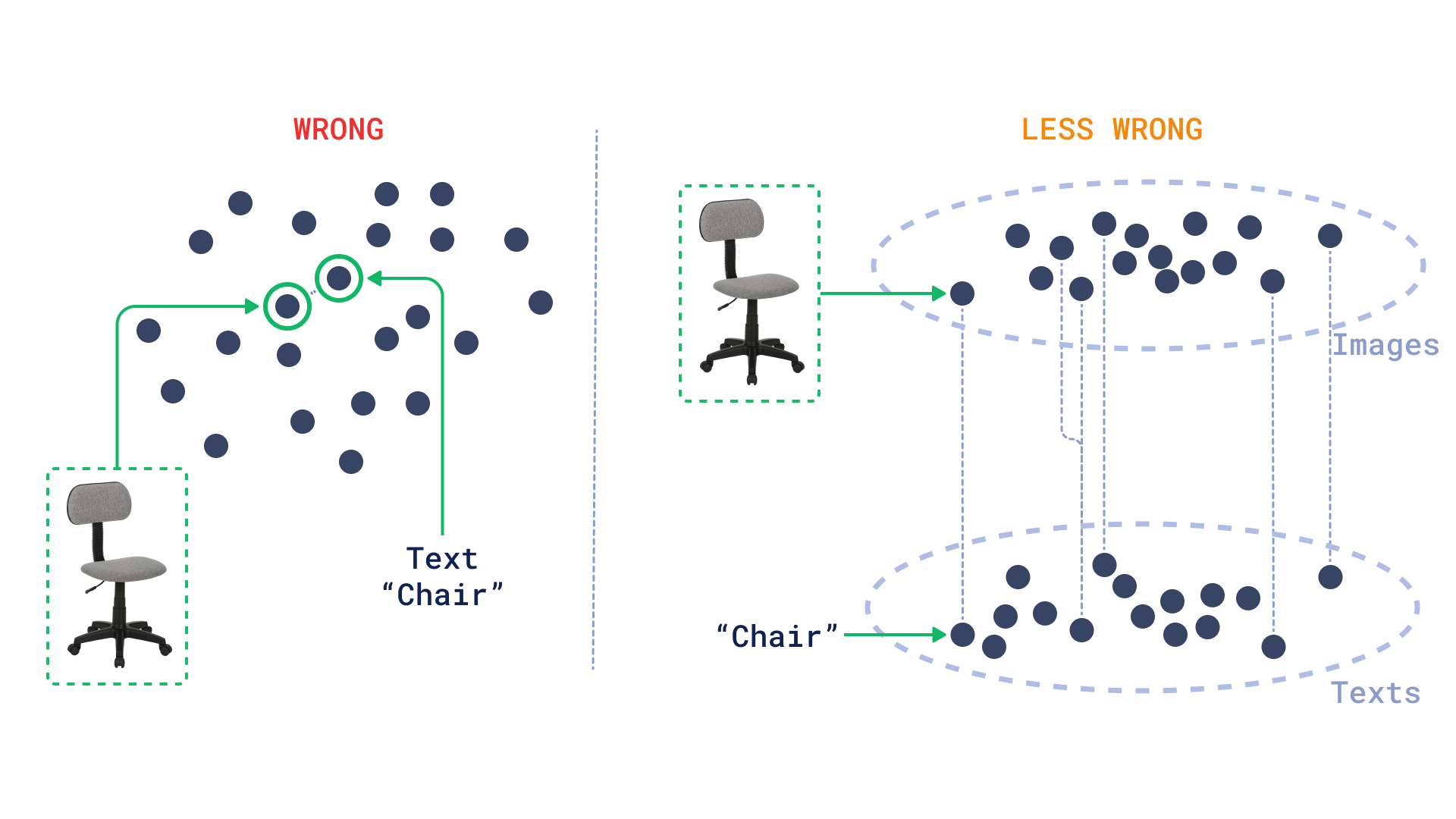
这就是发现的优势所在,因为它允许我们在考虑相同模式(图像)的同时,使用来自另一种模式(文本)的目标来约束空间。
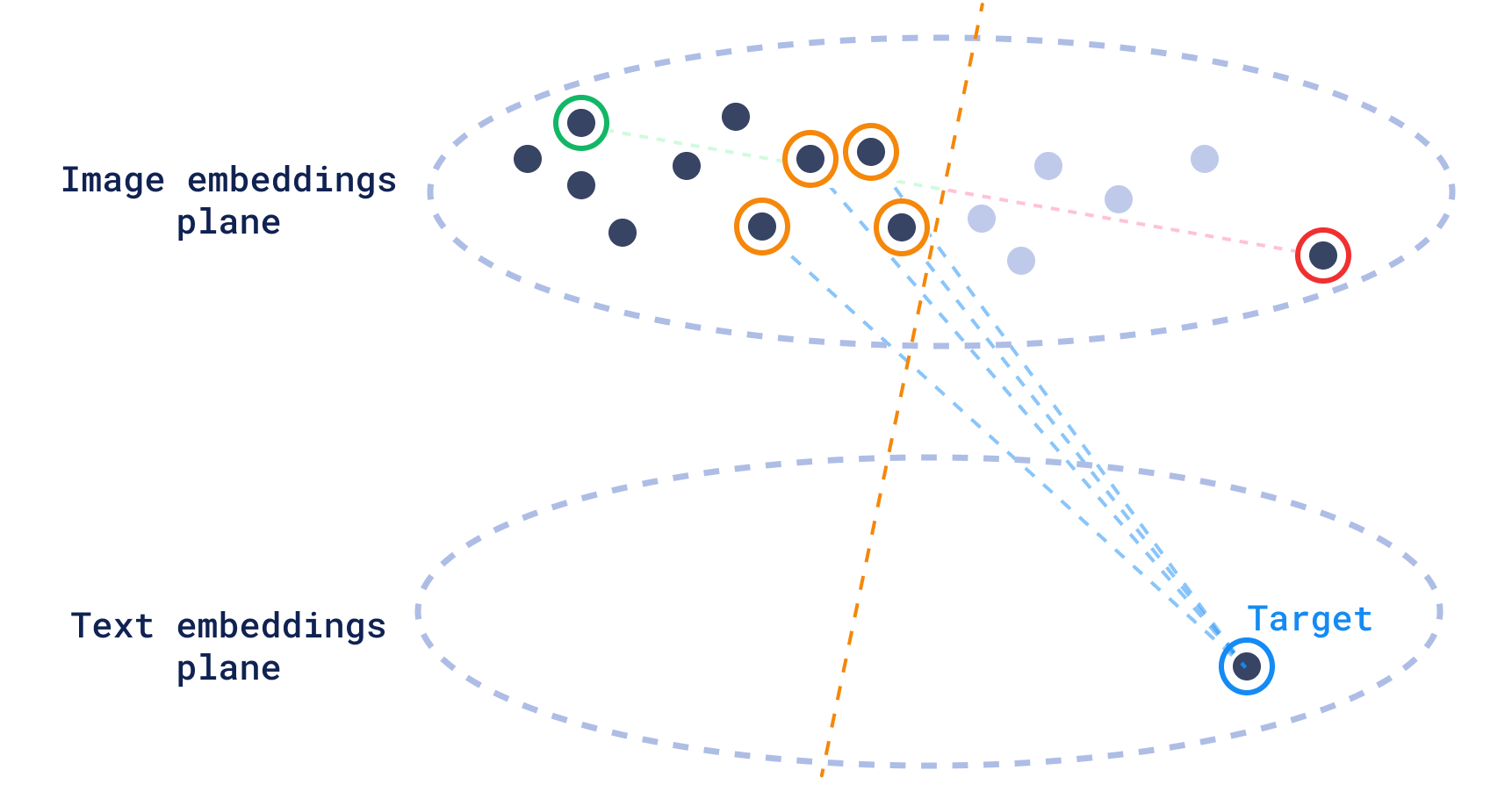
发现搜索还允许我们以更多上下文对的形式持续向搜索引擎提供反馈,这样我们就可以不断完善搜索,直到找到我们正在寻找的东西。
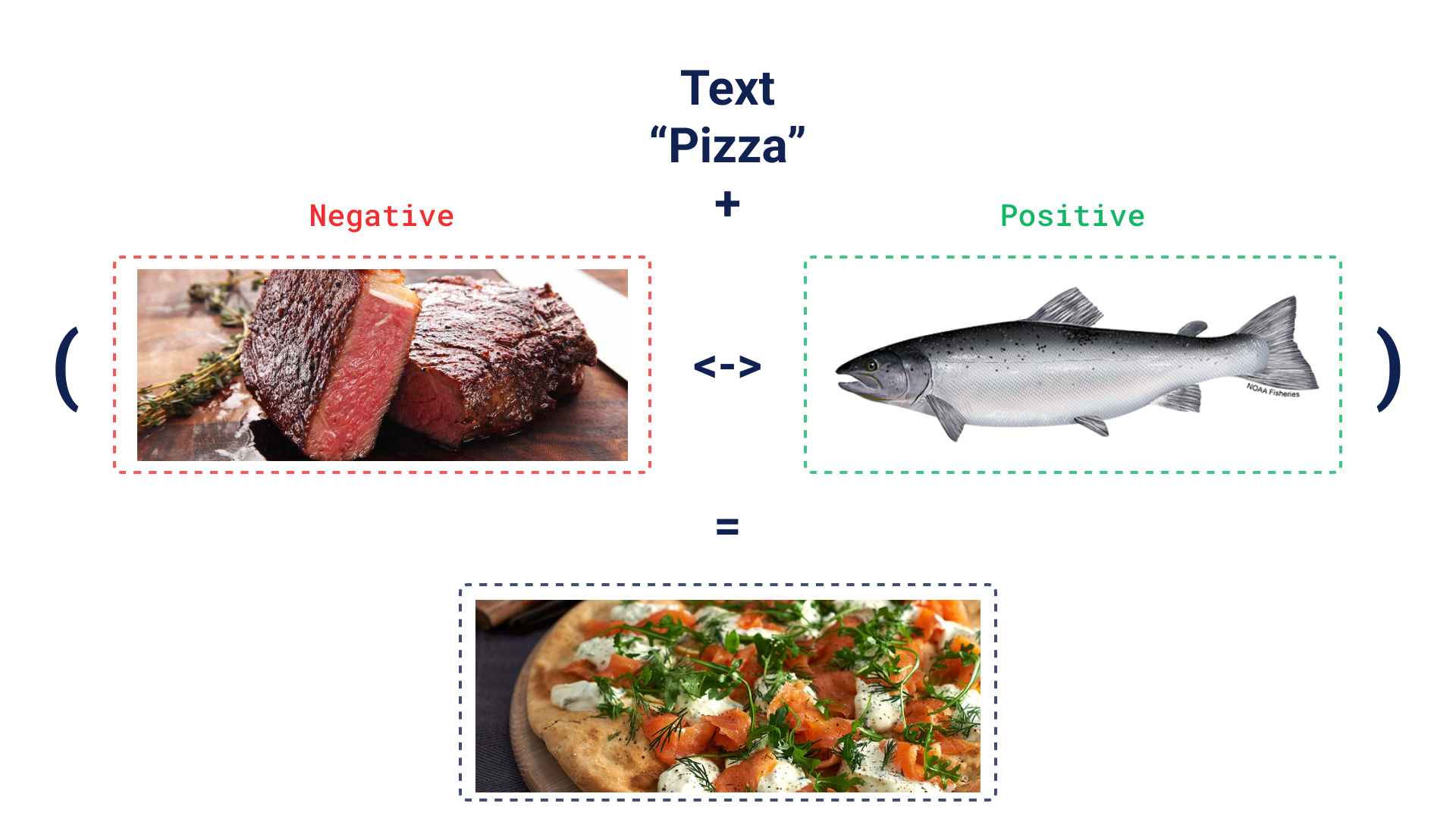
另一个直观的例子:想象您正在寻找一份鱼肉披萨,但披萨的名字可能令人困惑,所以您可以只输入“披萨”,并更喜欢鱼而不是肉。发现搜索将允许您使用这些输入来推荐鱼肉披萨……即使它不叫鱼肉披萨!
上下文搜索
现在,第二种情况:只提供上下文。
您是否曾在您最喜欢的音乐流媒体服务中陷入相同的推荐?这可能是因为陷入了相似性泡沫。随着用户输入的复杂性增加,多样性变得稀缺,并且变得更难强制系统推荐不同的东西。
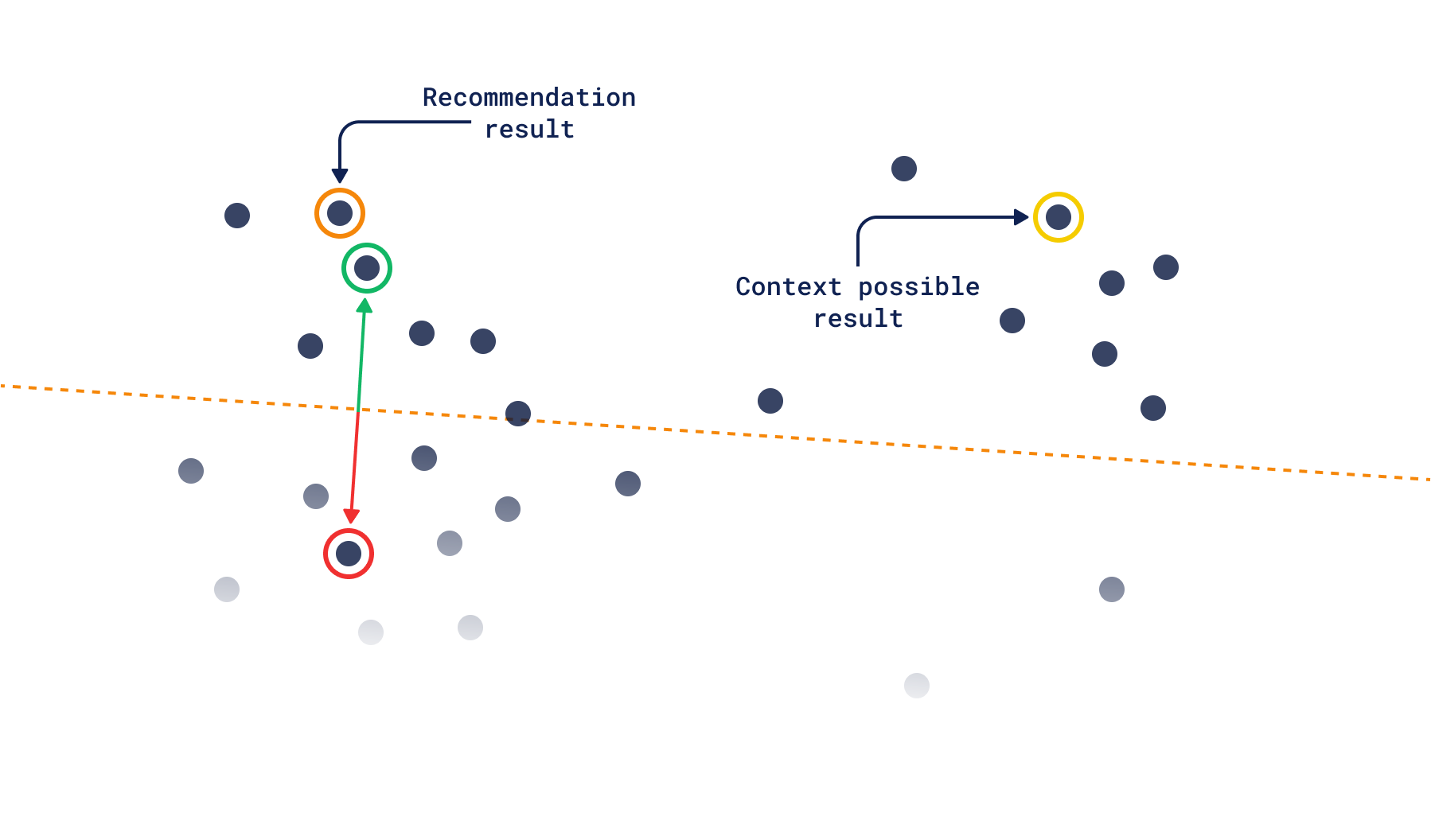
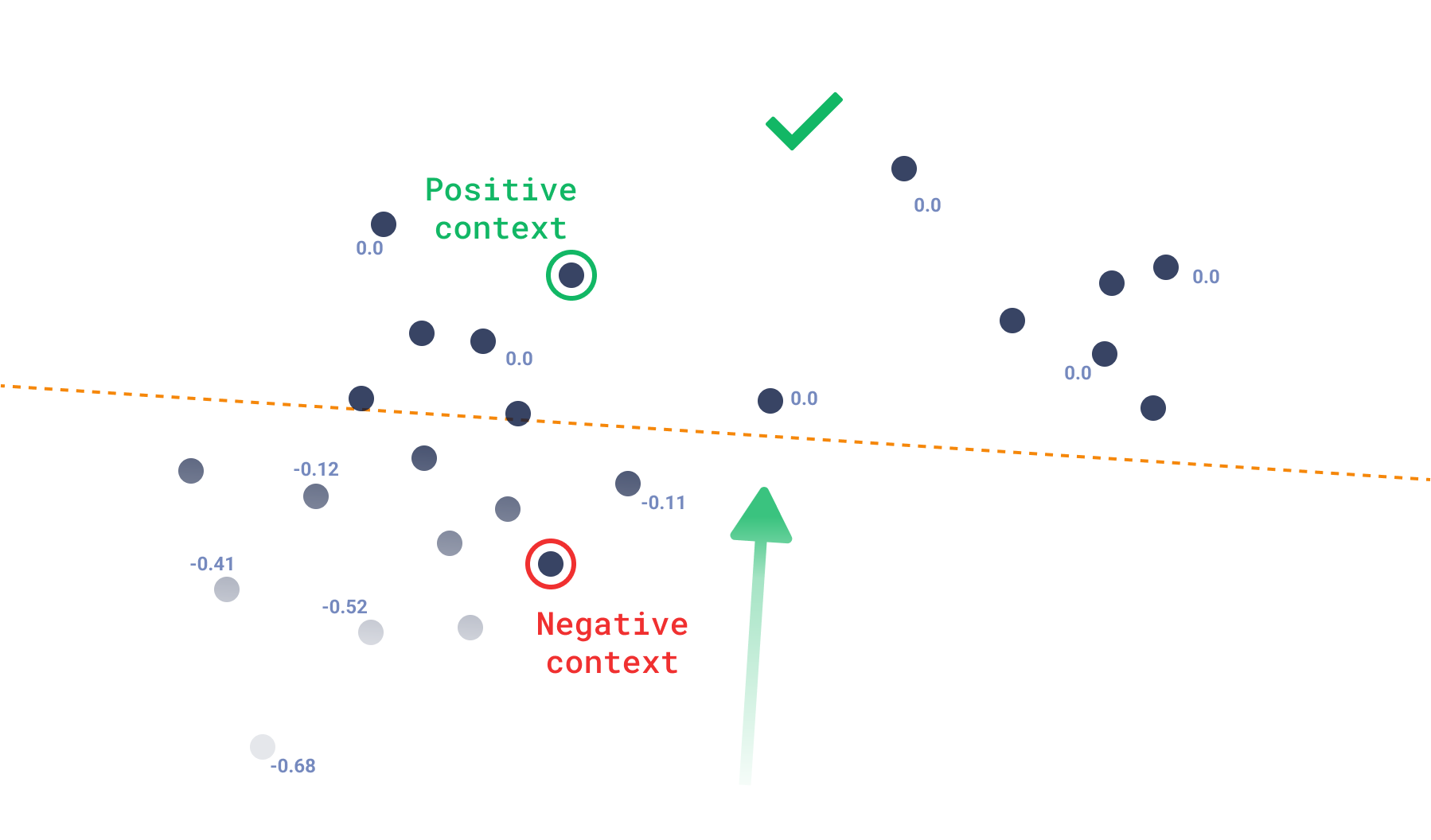
上下文搜索通过将搜索的焦点从单个点上移开来解决这个问题。相反,它从向量空间中某个区域内的随机点中进行选择。这种搜索受三元组损失的影响最大,因为得分可以被认为是“一个点比正向量更接近负向量的程度是多少?”。如果它更接近正向量,那么它的得分将为零,与同一区域内的任何其他点相同。但如果它在负侧,它将获得越来越负的得分,距离越远。
在处理高维空间时,创建复杂的偏好变得更容易,因为您只需向搜索中添加更多的上下文对。这样,您应该能够充分约束空间,从而从仅由输入中的上下文创建的每个搜索“类别”中选择点。
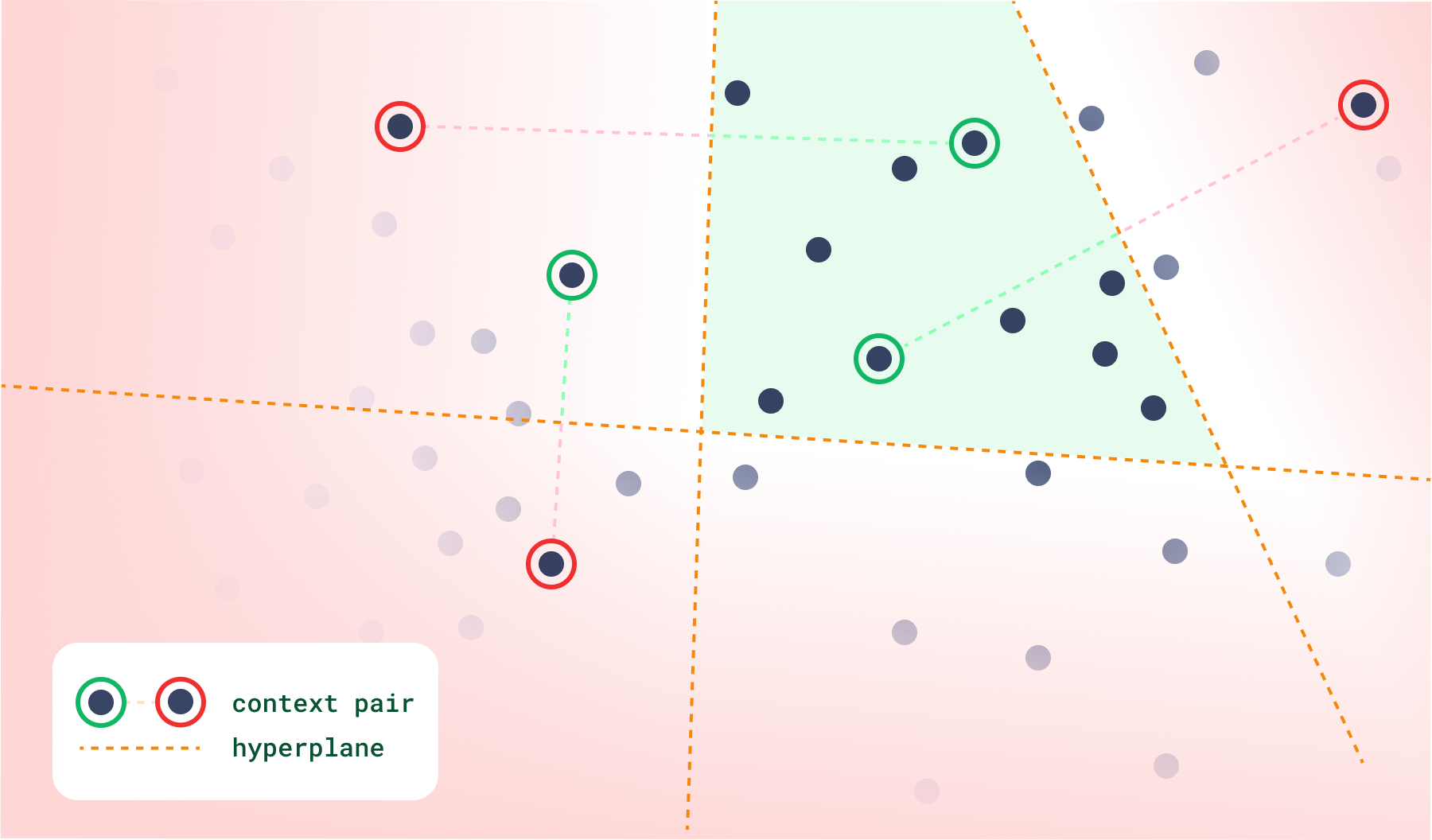
通过这种方式,您可以提供令人耳目一新的推荐,同时通过提供正向和负向反馈,甚至尝试不同对的排列来保持控制。
关键要点
- 发现搜索是向量空间中受控探索的强大工具。由正向量和负向量组成的上下文限制了搜索空间,而目标则指导搜索。
- 实际应用包括多模态搜索、多样化推荐和上下文驱动的探索。
- 准备好了解更多关于其背后的数学原理以及如何使用它吗?请查看文档

