隐藏结构
在处理大量文档、图像或其他非结构化数据数组时,了解整体情况通常会很有用。单独检查数据点并非总是理解数据结构的最佳方式。

没有上下文的数据点,基本没用
就像表格中的数字在绘制成图表时获得意义一样,可视化非结构化数据项之间的距离(相似/不相似)可以揭示隐藏的结构和模式。

可视化图表,非常直观
在许多实现中,距离矩阵计算是聚类或可视化过程的一部分,需要蛮力计算或构建临时索引。然而,使用 Qdrant,数据已经索引,并且可以相对便宜地计算距离矩阵。
在本文中,我们将使用距离矩阵 API 探索几种数据探索方法。
降维
最初,我们可能希望一眼就能可视化整个数据集,或者至少是其中一大部分。然而,高维数据无法直接可视化。我们必须应用降维技术将数据转换为低维表示,同时保留重要的数据属性。
在本文中,我们将使用 UMAP 作为我们的降维算法。
这是对 UMAP 的非常简化但直观的解释
- 在 2D 空间中随机生成点:为每个高维点分配一个随机的 2D 点。
- 计算高维点的距离矩阵:计算所有点对之间的距离。
- 计算 2D 点的距离矩阵:类似于步骤 2。
- 匹配两个距离矩阵:调整 2D 点以最小化差异。
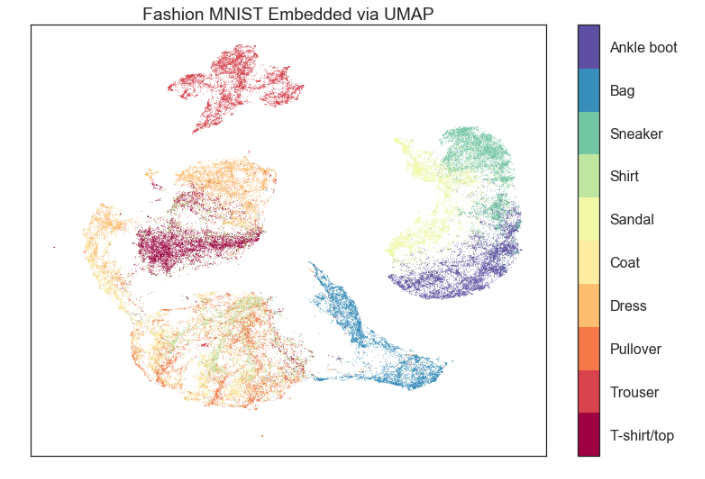
UMAP 结果的典型示例,来源
UMAP 保留了高维点之间的相对距离;实际坐标不是必需的。如果我们已经有了距离矩阵,则可以完全跳过步骤 2。
让我们使用 Qdrant 来计算距离矩阵并应用 UMAP。我们将使用一个非常适合在 Qdrant 中进行实验的默认数据集之一——Midjourney Styles 数据集。
使用此命令将数据集下载并导入到 Qdrant
PUT /collections/midlib/snapshots/recover
{
"location": "http://snapshots.qdrant.io/midlib.snapshot"
}
我们还需要准备我们的 Python 环境
pip install umap-learn seaborn matplotlib qdrant-client
导入必要的库
# Used to talk to Qdrant
from qdrant_client import QdrantClient
# Package with original UMAP implementation
from umap import UMAP
# Python implementation for sparse matrices
from scipy.sparse import csr_matrix
# For vizualization
import seaborn as sns
建立与 Qdrant 的连接
client = QdrantClient("https://:6333")
完成后,我们可以计算距离矩阵
# Request distances matrix from Qdrant
# `_offsets` suffix defines a format of the output matrix.
result = client.search_matrix_offsets(
collection_name="midlib",
sample=1000, # Select a subset of the data, as the whole dataset might be too large
limit=20, # For performance reasons, limit the number of closest neighbors to consider
)
# Convert distances matrix to python-native format
matrix = csr_matrix(
(result.scores, (result.offsets_row, result.offsets_col))
)
# Make the matrix symmetric, as UMAP expects it.
# Distance matrix is always symmetric, but qdrant only computes half of it.
matrix = matrix + matrix.T
现在我们可以将 UMAP 应用于距离矩阵
umap = UMAP(
metric="precomputed", # We provide ready-made distance matrix
n_components=2, # output dimension
n_neighbors=20, # Same as the limit in the search_matrix_offsets
)
vectors_2d = umap.fit_transform(matrix)
这就是获取数据 2D 表示所需的全部内容。
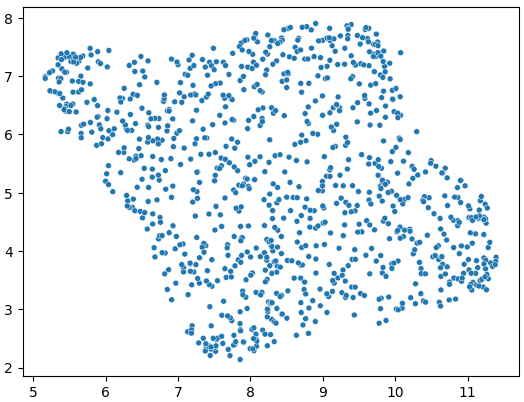
UMAP 应用于 Midlib 数据集
UMAP 并不是唯一与我们的距离矩阵 API 兼容的算法。例如,scikit-learn 还提供
- Isomap - 通过等距映射进行非线性降维。
- SpectralEmbedding - 根据指定函数形成亲和矩阵,并对相应的图拉普拉斯算子应用谱分解。
- TSNE - 著名的降维算法。
聚类
理解数据结构的另一种方法是聚类——对相似项进行分组。
请注意,没有普遍最佳的聚类准则或算法。
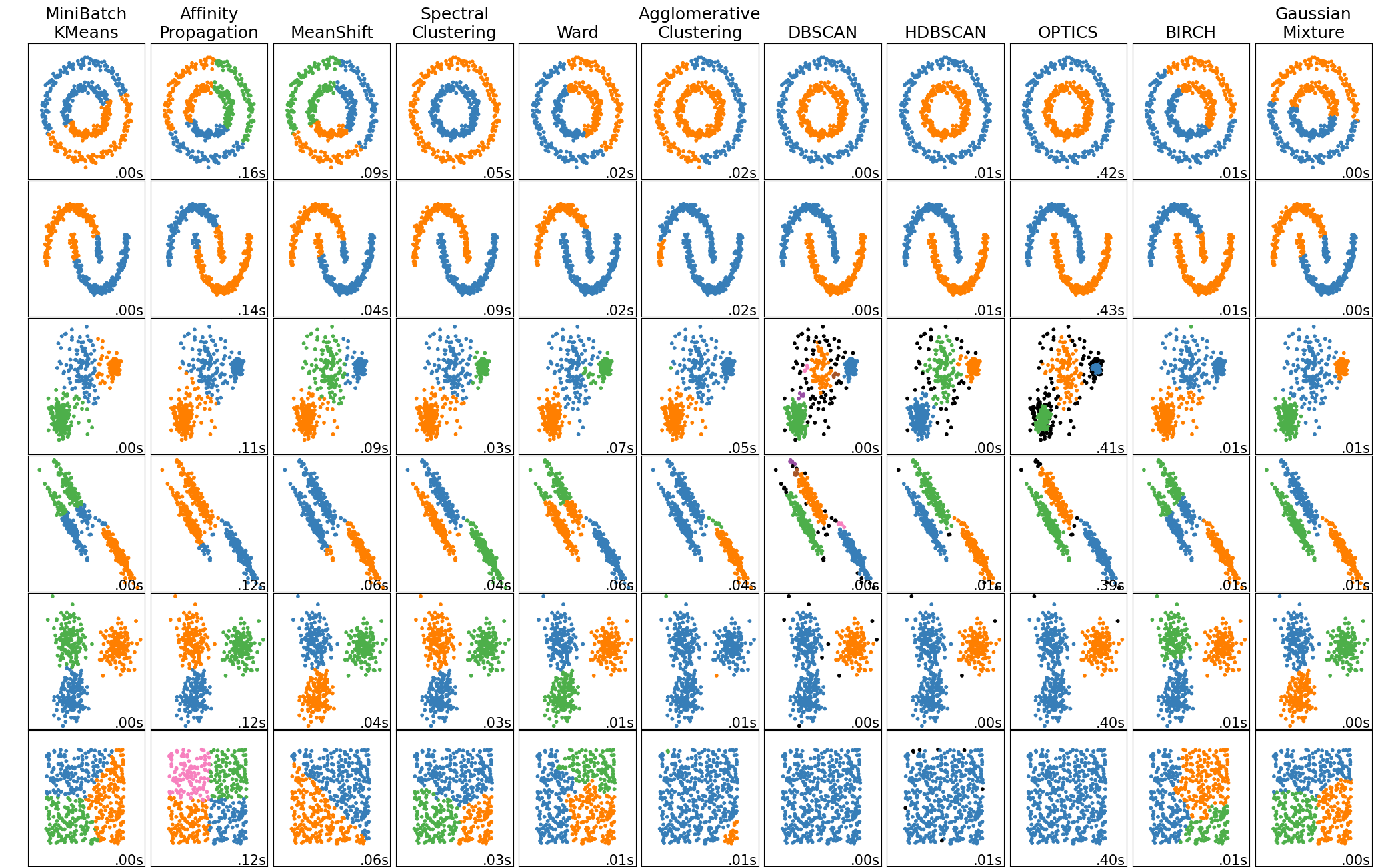
聚类示例,来源
许多聚类算法都接受预计算的距离矩阵作为输入,因此我们可以使用之前计算的相同距离矩阵。
让我们考虑一个使用 KMeans 算法聚类 Midlib 数据集的简单示例。
从 scikit-learn.cluster 文档中我们知道 KMeans 算法的 fit() 方法更喜欢作为输入
X : {array-like, sparse matrix} 形状 (n_samples, n_features):
要聚类的训练实例。需要注意的是,数据将被转换为 C 顺序,如果给定数据不是 C 连续的,这将导致内存复制。如果传入稀疏矩阵,如果它不是 CSR 格式,则会进行复制。
因此我们可以重用上一个示例中的 matrix
from sklearn.cluster import KMeans
# Initialize KMeans with 10 clusters
kmeans = KMeans(n_clusters=10)
# Generate index of the cluster each sample belongs to
cluster_labels = kmeans.fit_predict(matrix)
通过这段简单的代码,我们已经将数据聚类成 10 个簇,而过程中主要的 CPU 密集型部分由 Qdrant 完成。
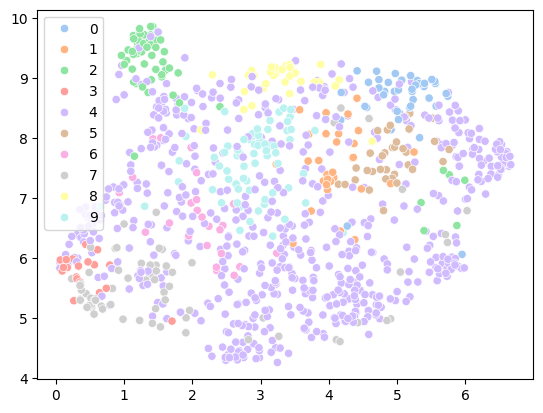
聚类应用于 Midlib 数据集
如何绘制此图表
sns.scatterplot(
# Coordinates obtained from UMAP
x=vectors_2d[:, 0], y=vectors_2d[:, 1],
# Color datapoints by cluster
hue=cluster_labels,
palette=sns.color_palette("pastel", 10),
legend="full",
)
图表
聚类和降维都旨在提供更透明的数据概览。然而,它们有一个共同的特点——它们需要在结果可视化之前进行训练步骤。
这也意味着引入新的数据点需要重新运行训练步骤,这可能会非常耗费计算资源。
图表提供了另一种数据探索方法,可以直接、交互式地可视化数据点之间的关系。在图表表示中,每个数据点都是一个节点,数据点之间的相似性表示为连接节点的边。
这样的图表可以使用 力导向图绘制 算法实时渲染,该算法旨在通过动态重新定位节点来最小化系统能量——数据点越相似,它们之间的边就越强。
向图表添加新的数据点就像插入新的节点和边一样简单,无需重新运行任何训练步骤。
实际上,一次性为整个数据集渲染图表可能耗费大量计算资源,并且用户难以承受。因此,让我们探讨一些解决此问题的策略。
从单个节点展开
这是最简单的方法,我们从一个节点开始,通过向图中添加最相似的节点来扩展图表。

数据的图表示
从集合中采样
如果您想探索单个点的邻居,展开单个节点效果很好,但如果您想探索整个数据集怎么办?如果您的数据集足够小,您可以一次性渲染所有数据点的关系。但这在实践中很少见。
相反,我们可以对数据子集进行采样,并为该子集渲染图表。这样,我们可以很好地概览数据,而不会让用户被过多的信息淹没。
让我们尝试在 Qdrant 的图表探索工具中这样做
{
"limit": 5, # node neighbors to consider
"sample": 100 # nodes
}

数据的图表示 (Qdrant 的图表探索工具)
此图表捕获了一些数据的高级结构,但您可能已经注意到,它相当嘈杂。这是因为相似性差异相对较小,并且可能被力导向布局算法的拉伸和压缩所淹没。
为了使图表更具可读性,让我们专注于最重要的相似性并构建所谓的 最小/最大生成树。
{
"limit": 5,
"sample": 100,
"tree": true
}
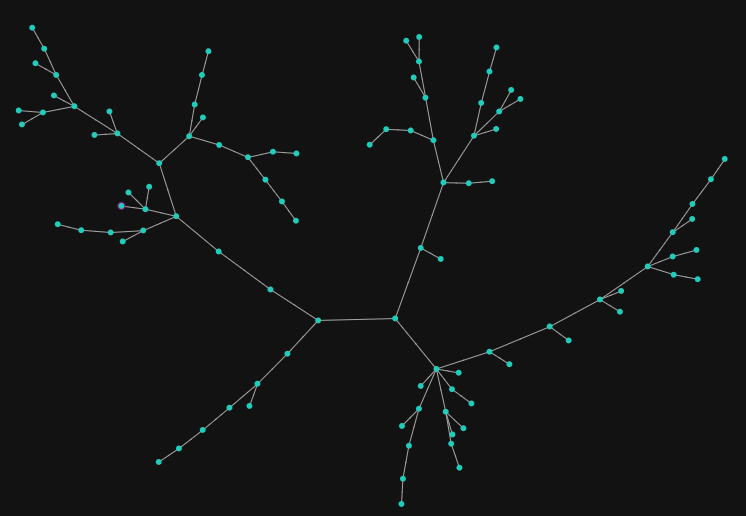
图表的生成树 (Qdrant 的图表探索工具)
该算法将只保留最重要的边并删除其余的边,同时保持图表的连通性。通过这样做,我们可以揭示数据簇及其之间最重要的关系。
从某种意义上说,这类似于层次聚类,但能够交互式地探索数据。另一个类比可能是动态构建的思维导图。
结论
向量相似性不仅仅是查找最近的邻居——它为数据探索提供了一个强大的工具。许多算法可以构建人类可读的数据表示,而 Qdrant 使使用它们变得容易。
Qdrant Web UI (可视化和图表探索工具) 中提供了多种数据探索工具,对于更高级的用例,您可以直接利用我们的距离矩阵 API。
使用您的数据尝试一下,看看您能揭示出哪些隐藏结构!

