如果您需要在向量空间中找到一些相似的对象,例如由嵌入或匹配的神经网络提供,您可以选择各种库:Annoy、FAISS 或 NMSLib。所有这些都将在几乎任何空间中为您提供快速的近似邻居搜索。
但是,如果您的搜索需要引入一些限制呢?例如,您只想搜索某个类别的产品,或者选择某个特定品牌最相似的客户。我没有找到任何简单的解决方案。有一些讨论,例如这个,但它们只建议遍历顶部搜索结果并在搜索后相应地应用条件。
让我们看看是否可以修改任何 ANN 算法,以便在搜索过程中应用约束。
Annoy 在随机投影上构建树索引。树索引意味着我们将遇到关系数据库中出现的问题:如果字段索引是独立构建的,那么一次只能使用其中一个。由于以前没有人解决过这个问题,所以似乎没有简单的方法。
基准测试上显示了最佳结果的另一种算法。它被称为 HNSW,代表分层可导航小世界。
原始论文写得很好,非常易读,所以我在这里只给出主要思想。我们需要在所有索引点之间构建一个导航图,以便在此图上进行贪婪搜索将引导我们找到最近的点。该图是通过顺序添加与先前添加的点通过固定数量的边连接的点来构建的。在生成的图中,每个点的边数不超过给定阈值 $m$,并且总是包含最近的考虑点。
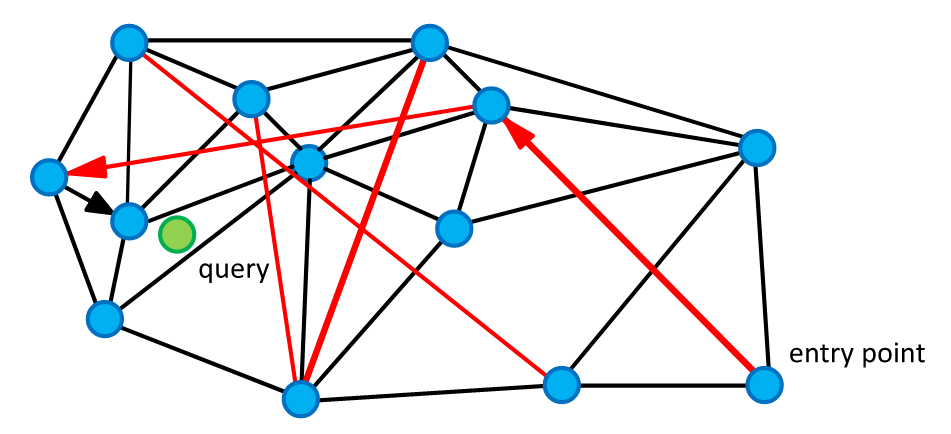
我们如何修改它?
如果我们简单地将过滤条件应用于此图的节点,并在贪婪搜索中仅使用符合这些条件的节点呢?事实证明,即使是这种天真的修改算法也可以涵盖某些用例。
一种这样的情况是,如果您的标准与向量语义不相关。例如,您使用向量搜索服装名称并希望过滤掉某些尺寸。在这种情况下,节点将从整个集群结构中均匀过滤掉。因此,渗流理论中获得的理论结论变得适用
渗流与图的鲁棒性(也称为网络)有关。给定一个包含 $n$ 个节点和平均度数 $\langle k\rangle$ 的随机图。接下来,我们随机删除 $1-p$ 的节点,只保留 $p$ 的节点。存在一个临界渗流阈值 $pc = \frac{1}{\langle k\rangle}$,低于该阈值网络将碎片化,而高于 $pc$ 则存在一个巨大的连通分量。
该声明也通过实验证实
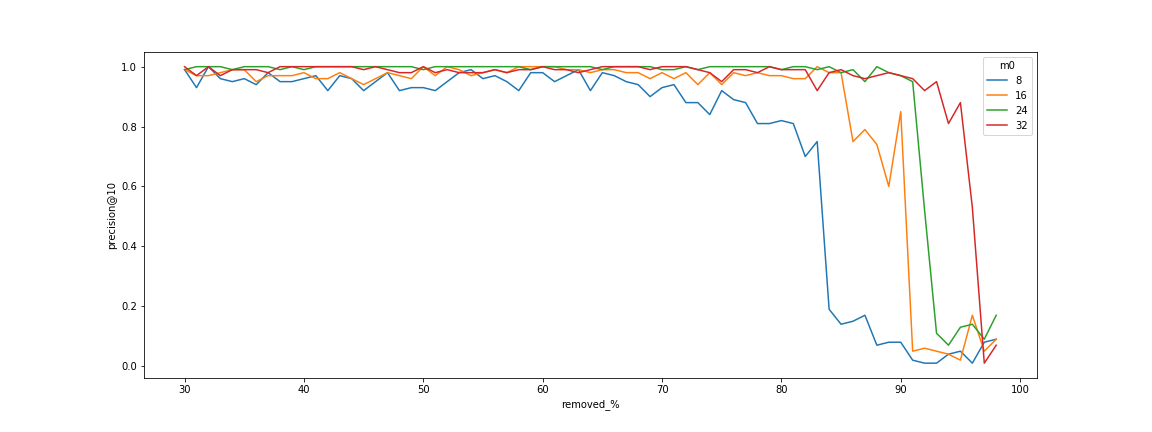
连通性对边数的依赖关系
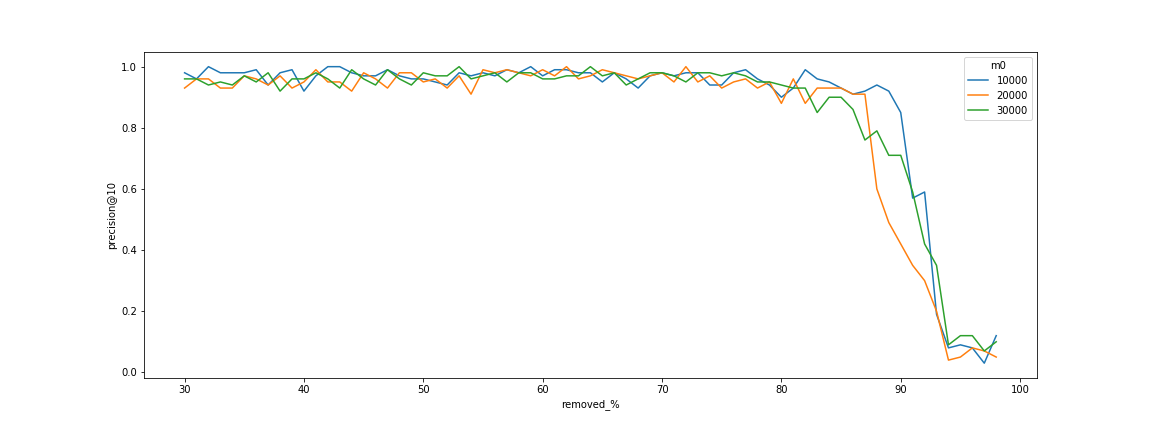
连通性对点数的依赖关系(无依赖关系)。
当搜索开始失败时,存在一个明显的阈值。此阈值是由于图分解为小的连通分量。图表还显示,可以通过增加算法的 $m$ 参数来移动此阈值,该参数负责节点的度数。
让我们考虑一些我们可能希望在搜索中应用的其他过滤条件
- 分类过滤
- 仅选择特定类别中的点
- 选择属于特定类别子集的点
- 选择具有特定标签集的点
- 数值范围
- 在某个地理区域内选择
在第一种情况下,我们可以简单地通过使用相同的图构建算法在每个类别内单独创建额外的边,然后将它们组合到原始图中,从而保证 HNSW 图是连通的。在这种情况下,总边数将不会增加超过 2 倍,无论类别数量如何。
第二种情况稍微困难一些。如果两个类别位于不同的簇中,它们之间的连接可能会丢失。
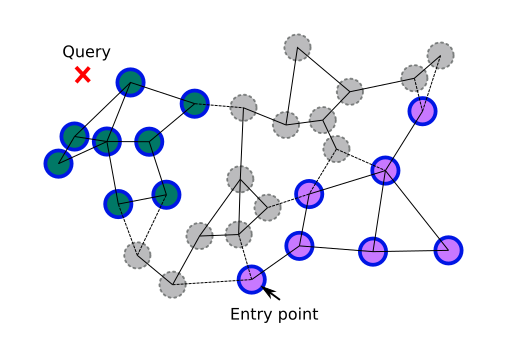
这里的想法是构建相同的导航图,但不是在节点之间,而是在类别之间。两个类别之间的距离可以定义为类别入口点之间的距离(或者,为了精确,定义为随机样本之间的平均距离)。现在我们可以通过排除的类别数量(而不是节点数量)来估计预期的图连通性。它仍然不能保证两个随机类别是连通的,但如果连通性阈值通过,它允许我们切换到每个类别中的多次搜索。在某些情况下,如果利用并行处理,多次搜索甚至可以更快。
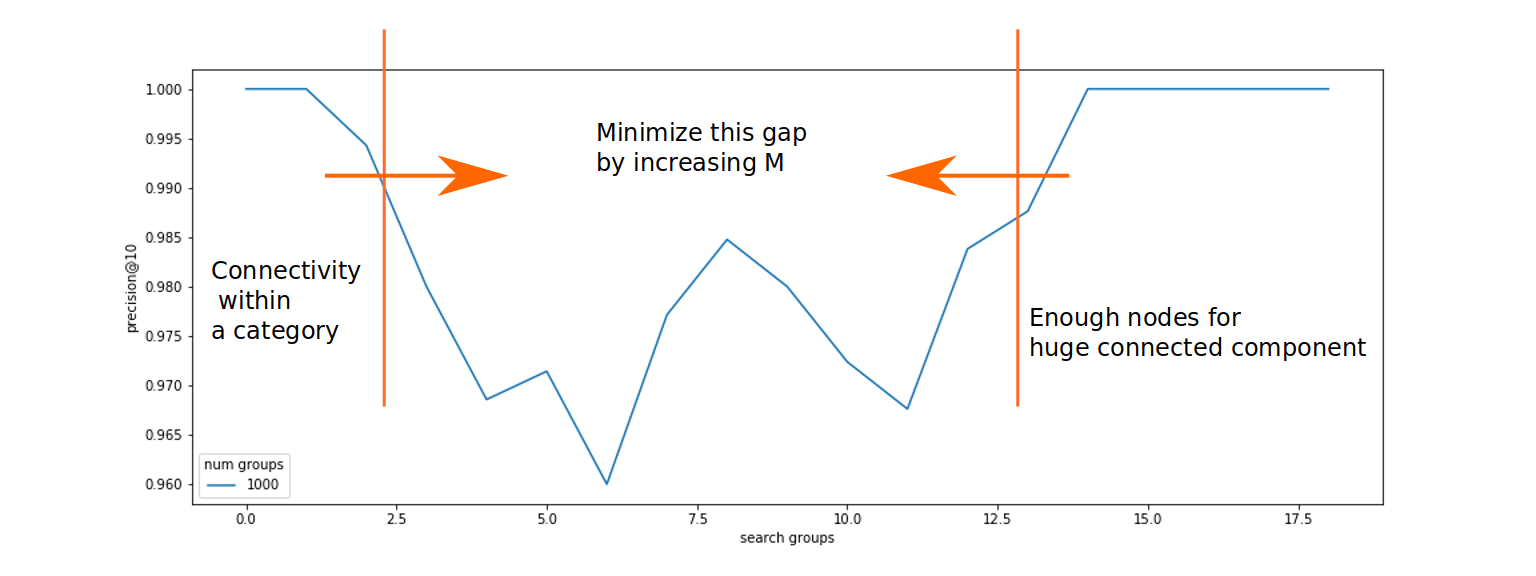
连通性对搜索中包含的随机类别的依赖关系
第三种情况可以通过与经典数据库中相同的方式解决。根据标记子集大小比率,我们可以选择以下场景之一
- 如果至少有一个子集很小:对包含最小子集的标签执行搜索,然后相应地过滤点。
- 如果大子集产生大交集:执行带约束的常规搜索,预期交集大小符合连通性阈值。
- 如果大子集产生小交集:对交集执行线性搜索,预期它足够小以适应时间范围。
数值范围案例可以归结为前一种情况,如果我们将其分成包含相等数量点的桶。接下来,我们还将相邻的桶连接起来以实现图的连通性。我们仍然需要过滤一些位于边界桶但未满足实际约束的结果,但它们的数量可以通过桶的大小来调节。
地理案例与数值案例非常相似。通常的地理搜索涉及地理哈希,它将任何地理点匹配到固定长度的标识符。
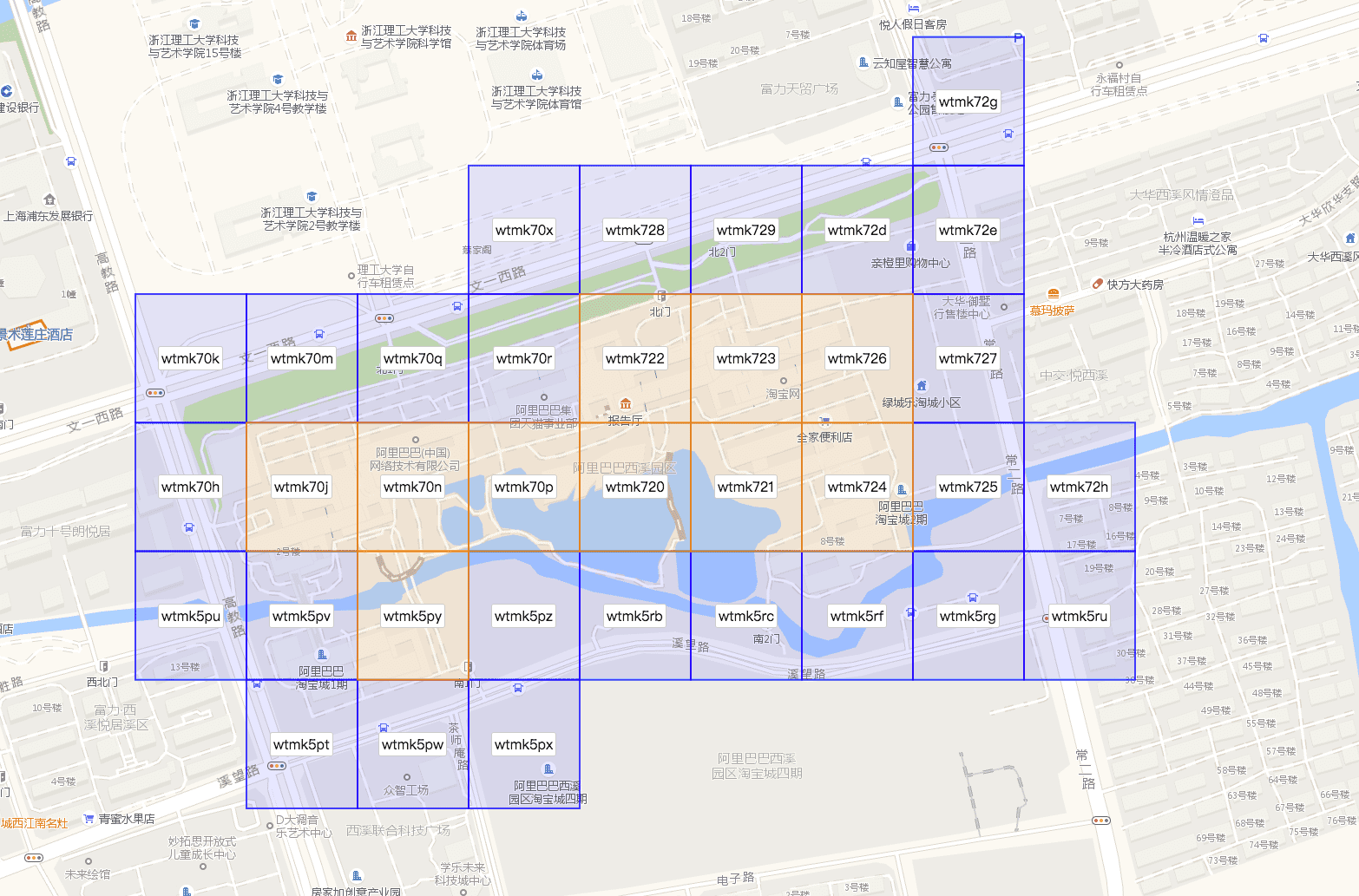
我们可以将这些标识符用作类别,并额外在相邻的地理哈希之间建立连接。这将确保任何选定的地理区域也将包含连接的 HNSW 图。
结论
可以改进 HNSW 算法,使其在第一搜索阶段支持过滤点。过滤可以根据属于类别进行,这又推广到数值范围和地理等流行情况。

