乘积量化揭秘:简化数据管理效率
Qdrant 1.1.0 版本带来了对标量量化的支持,这是一种通过使用int8来表示通常由float32表示的值,从而将内存占用减少四倍的技术。
向量搜索中的内存使用甚至可以进一步减少!欢迎使用 Qdrant 1.2.0 的全新功能——乘积量化!
什么是乘积量化?
乘积量化像其他所有量化方法一样,将浮点数转换为整数。然而,这个过程比标量量化稍微复杂,并且更具可定制性,因此您可以在内存使用和搜索精度之间找到最佳平衡点。本文涵盖了执行乘积量化所需的所有步骤以及其在 Qdrant 中的实现方式。
乘积量化如何工作?
假设我们正在向集合中添加一些向量,并且我们的优化器决定开始创建一个新的分段。

将向量切片
首先,我们的向量将被分成块,也就是子向量。块的数量是可配置的,但根据经验法则,块的数量越少,压缩率越高。这也会降低搜索精度,但在某些情况下,您可能希望将内存使用保持在最低水平。

Qdrant API 允许选择 4 倍到 64 倍的压缩比。在我们的示例中,我们选择了 16 倍,因此每个子向量将由 4 个浮点数(16 字节)组成,最终将由单个字节表示。
聚类
然后,我们向量的块被用作聚类的输入。Qdrant 使用 K-means 算法,其中 $ K = 256 $。这是预先选择的,因为这是一个字节所能表示的最大值数量。结果,我们为每个块收到一个包含 256 个质心的列表,并为每个质心分配一个唯一的 ID。聚类是为每组块单独完成的。
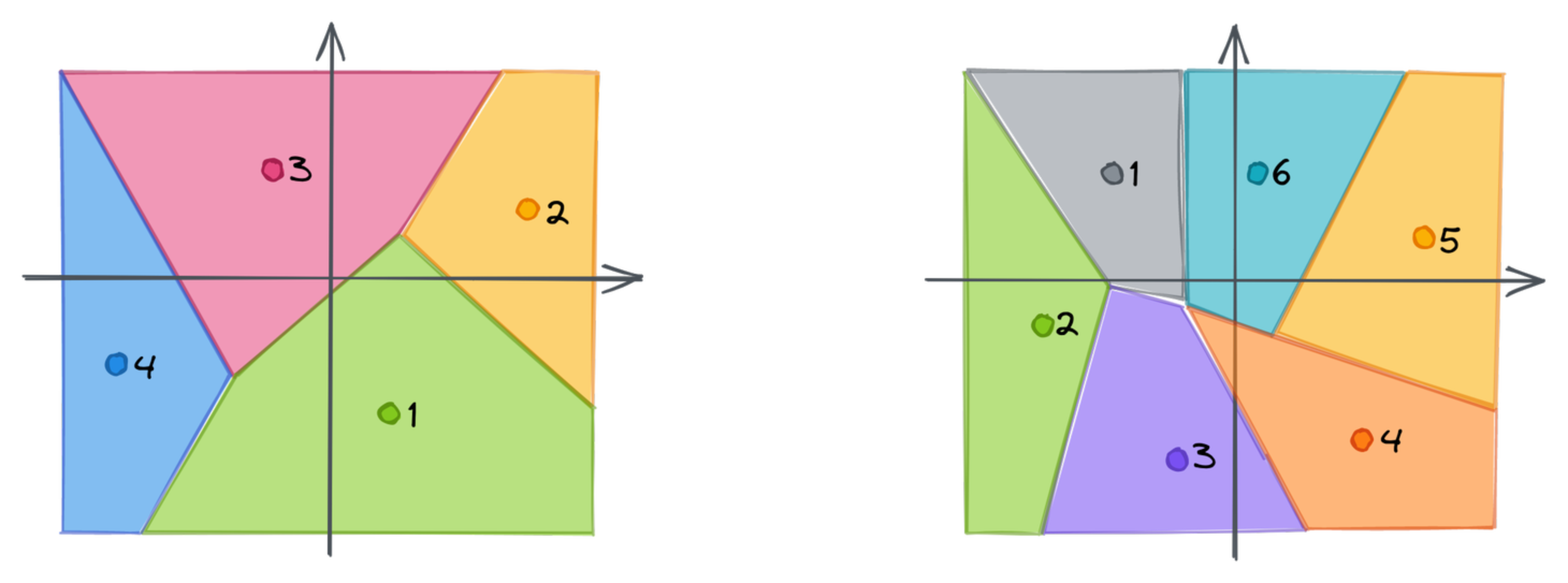
向量的每个块现在可以映射到最近的质心。这就是我们失去精度的地方,因为单个点将只代表一个完整的子空间。我们不再使用子向量,而是可以存储最近质心的 ID。如果我们将此操作对每个块重复,我们可以将原始嵌入近似为由质心的后续 ID 组成的向量。创建的向量的维度等于块的数量,在我们的例子中是 2。

完整过程
所有这些步骤构建了以下乘积量化流程
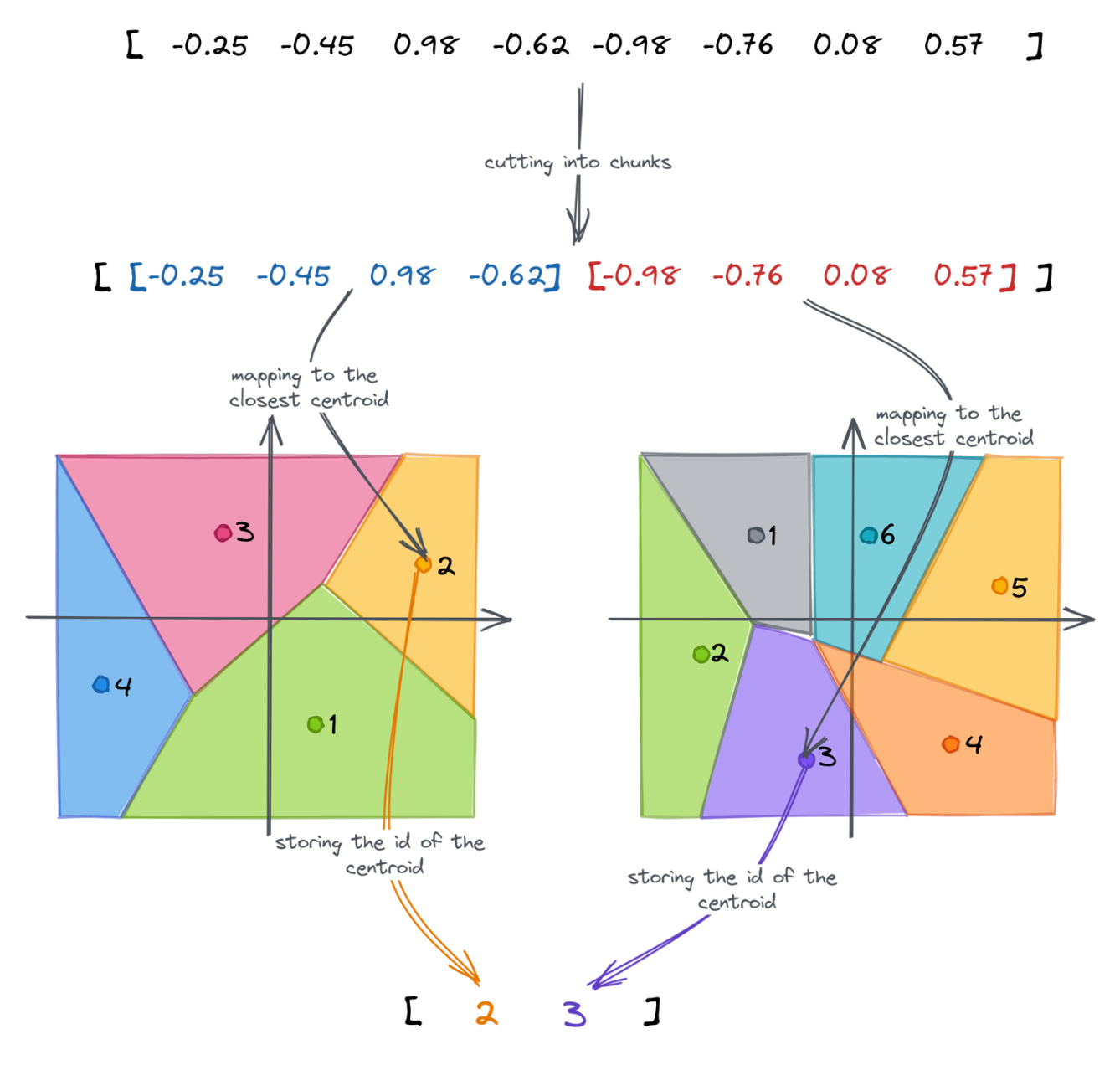
测量距离
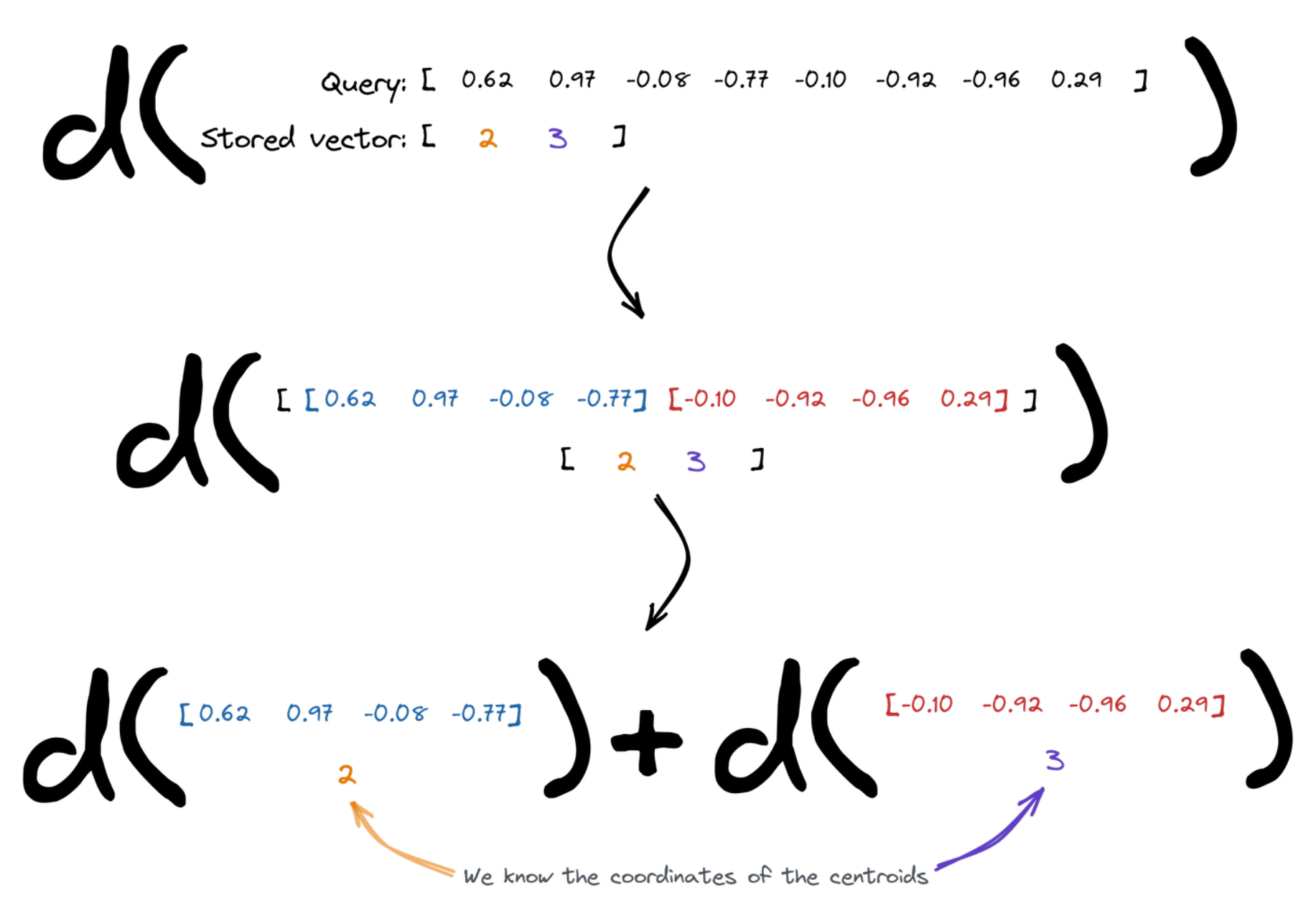
向量搜索依赖于点之间的距离。启用乘积量化会稍微改变其计算方式。查询向量被分成块,然后我们将总距离计算为子向量与分配给我们要比较的向量的特定 ID 的质心之间的距离之和。我们知道质心的坐标,所以这很容易。
Qdrant 实现
搜索操作需要计算到多个点的距离。由于我们计算的是到有限质心集的距离,因此这些质心可以预先计算并重复使用。Qdrant 为每个查询创建一个查找表,因此它可以简单地将几个项相加来测量查询与所有质心之间的距离。
| 质心 0 | 质心 1 | ... | |
|---|---|---|---|
| 块 0 | 0.14213 | 0.51242 | |
| 块 1 | 0.08421 | 0.00142 | |
| ... | ... | ... | ... |
乘积量化基准测试
乘积量化伴随着一定的代价——需要执行一些额外的操作,因此性能可能会降低。然而,内存使用也可能大幅减少。像往常一样,我们进行了一些基准测试,以便您对预期结果有一个简要的了解。
我们再次重用了与我们发布的其他基准测试相同的管道。我们选择了Arxiv-titles-384-angular-no-filters和Glove-100数据集来衡量乘积量化对精度和时间的影响。两次实验均在 $ EF = 128 $ 下启动。结果汇总在表格中
Glove-100
| 原始 | 1D 簇 | 2D 簇 | 3D 簇 | |
|---|---|---|---|---|
| 平均精度 | 0.7158 | 0.7143 | 0.6731 | 0.5854 |
| 平均搜索时间 | 2336 微秒 | 2750 微秒 | 2597 微秒 | 2534 微秒 |
| 压缩率 | x1 | x4 | x8 | x12 |
| 上传和索引时间 | 147 秒 | 339 秒 | 217 秒 | 178 秒 |
乘积量化增加了索引和搜索时间。压缩比越高,搜索精度越低。主要优点无疑是内存使用量减少。
Arxiv-titles-384-angular-no-filters
| 原始 | 1D 簇 | 2D 簇 | 4D 簇 | 8D 簇 | |
|---|---|---|---|---|---|
| 平均精度 | 0.9837 | 0.9677 | 0.9143 | 0.8068 | 0.6618 |
| 平均搜索时间 | 2719 微秒 | 4134 微秒 | 2947 微秒 | 2175 微秒 | 2053 微秒 |
| 压缩率 | x1 | x4 | x8 | x16 | x32 |
| 上传和索引时间 | 332 秒 | 921 秒 | 597 秒 | 481 秒 | 474 秒 |
事实证明,在某些情况下,乘积量化不仅可以减少内存使用,还可以减少搜索时间。
乘积量化 vs 标量量化
与标量量化相比,乘积量化提供了更高的压缩率。然而,这伴随着精度和有时内存中搜索速度的显著权衡。
乘积量化倾向于在某些特定场景中受到青睐
- 在低内存环境中部署,其中限制因素是磁盘读取次数而不是向量比较本身
- 原始向量维度足够高的情况
- 索引速度不是关键因素的情况
在不符合上述情况的情况下,应优先选择标量量化。
使用 Qdrant 进行乘积量化
如果您已经是 Qdrant 用户,我们提供了关于乘积量化的文档,它将帮助您为数据设置和配置新的量化,实现高达 64 倍的内存缩减。
准备好体验乘积量化的强大功能了吗?立即注册免费的 Qdrant 演示,优化您的数据管理!

