返回 Qdrant 内部原理

标量量化：背景、实践及更多 | Qdrant

Kacper Łukawski

·

2023年3月27日

释放效率：标量量化的力量

高维向量嵌入可能非常占用内存，尤其是在处理包含数百万个向量的大型数据集时。当我们扩大规模时，内存占用真正成为一个问题。存储单个数字所使用的数据类型的简单选择，即使是数十亿个数字，也会影响内存需求并使其变得惊人。数据类型的精度越高，您表示数字就越准确。向量越准确，距离计算就越精确。但是，当您需要更多的内存时，这些优势就不再划算了。

Qdrant 选择 float32 作为存储嵌入数字的默认类型。因此，单个数字需要 4 字节内存，一个 512 维向量占用 2 kB。这只是存储向量所需的内存。HNSW 图也有开销，因此根据经验法则，我们使用以下公式估算内存大小：

memory_size = 1.5 * number_of_vectors * vector_dimension * 4 bytes

虽然 Qdrant 提供了多种选项将部分数据存储在磁盘上，但从 1.1.0 版本开始，您还可以通过压缩嵌入来优化内存。我们已经实现了标量量化机制！事实证明，它不仅对内存有积极影响，而且对性能也有影响。

标量量化

标量量化是一种数据压缩技术，将浮点值转换为整数。在 Qdrant 中，float32 被转换为 int8，因此单个数字所需的内存减少了 75%。但这不仅仅是简单的四舍五入！这是一个使转换部分可逆的过程，因此我们也可以将整数转换回浮点数，但会有一点精度损失。

理论背景

假设我们有一个 float32 向量集合，并将单个值表示为 f32。实际上，神经网络嵌入并不覆盖浮点数表示的整个范围，而是覆盖一个小子范围。由于我们知道所有其他向量，我们可以建立所有数字的一些统计信息。例如，值的分布通常是正态的。

我们的示例显示，99% 的值来自 [-2.0, 5.0] 范围。转换为 int8 肯定会损失一些精度，因此我们宁愿将表示精度保持在 99% 最可能值的范围内，而忽略离群值的精度。实际上，范围宽度可能有不同的选择，可以是 [0, 1] 范围内的任何值，其中 0 表示空范围，而 1 将保留所有值。这是该过程的一个超参数，称为 quantile。0.95 或 0.99 通常是合理的选择，但一般来说，quantile ∈ [0, 1]。

转换为整数

让我们谈谈转换为 int8。整数也有一个可以表示的有限值集合。在一个字节内，它们可以表示多达 256 个不同的值，范围可以是 [-128, 127] 或 [0, 255]。

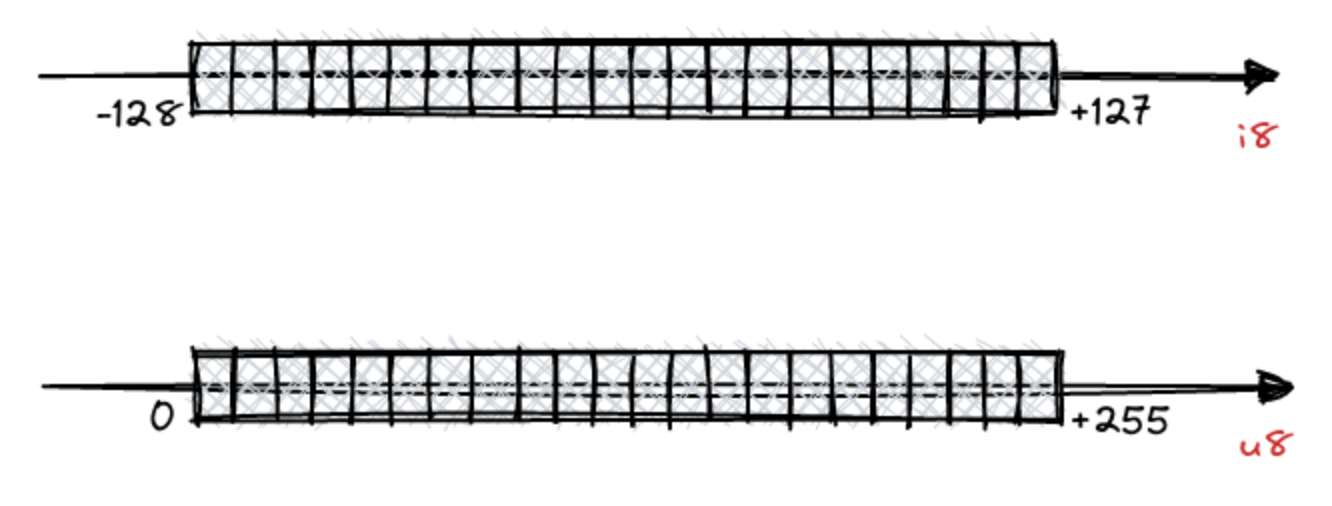
由于我们对 f32 可以表示的数字设置了一些边界，并且 i8 也有一些自然的边界，因此在这两个范围之间转换值的过程非常自然：

$$ f32 = \alpha \times i8 + offset $$

$$ i8 = \frac{f32 - offset}{\alpha} $$

参数 $ \alpha $ 和 $ offset $ 必须针对给定的一组向量进行计算，但这很容易做到，只需将 f32 和 i8 表示范围的最小值和最大值代入即可。

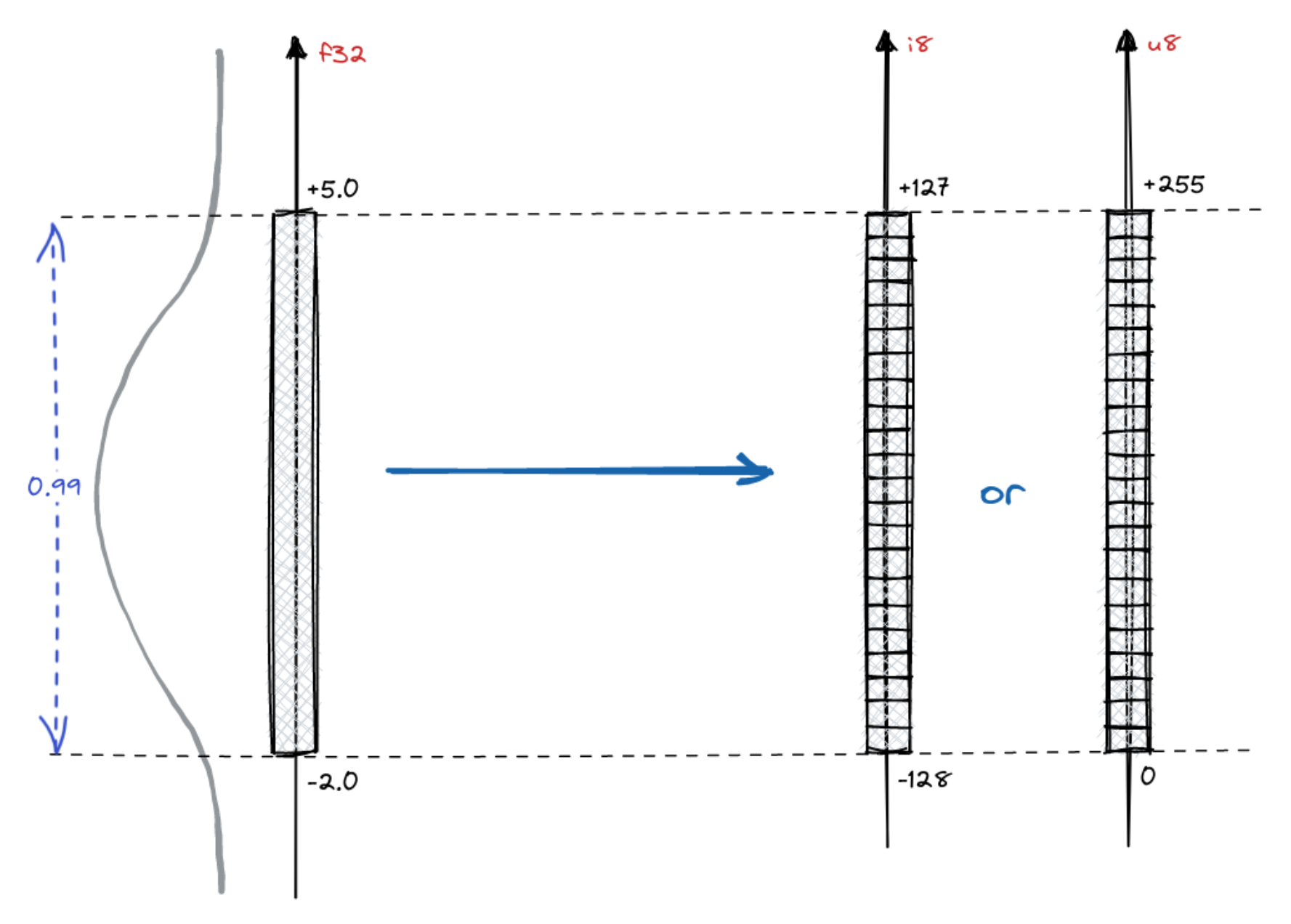
对于无符号 int8，计算如下：

$$ \begin{equation} \begin{cases} -2 = \alpha \times 0 + offset \\ 5 = \alpha \times 255 + offset \end{cases} \end{equation} $$

对于有符号 int8，我们只需更改表示范围的边界：

$$ \begin{equation} \begin{cases} -2 = \alpha \times (-128) + offset \\ 5 = \alpha \times 127 + offset \end{cases} \end{equation} $$

对于任何一组向量值，我们都可以简单地计算出 $ \alpha $ 和 $ offset $，并且这些值必须与集合一起存储，以便能够在这两种类型之间进行转换。

距离计算

我们存储集合中的向量不是用 int8 代替 float32 仅仅为了压缩内存。而是在计算向量之间的距离时会用到坐标。点积和余弦距离都需要将两个向量的对应坐标相乘，因此这是我们在 float32 上经常执行的操作。如果我们转换为 int8，它将是这样的：

$$ f32 \times f32’ = $$ $$ = (\alpha \times i8 + offset) \times (\alpha \times i8’ + offset) = $$ $$ = \alpha^{2} \times i8 \times i8’ + \underbrace{offset \times \alpha \times i8’ + offset \times \alpha \times i8 + offset^{2}}_\text{pre-compute} $$

第一个项 $ \alpha^{2} \times i8 \times i8’ $ 在测量距离时必须计算，因为它取决于两个向量。然而，第二个项和第三个项（分别为 $ offset \times \alpha \times i8’ $ 和 $ offset \times \alpha \times i8 $）仅取决于单个向量，这些可以预先计算并为每个向量保留。最后一个项 $ offset^{2} $ 不依赖于任何值，因此甚至可以计算一次并重复使用。

如果我们必须计算所有项来测量距离，性能甚至可能比不转换时更差。但由于我们可以预先计算大部分项，事情变得更简单了。事实证明，标量量化不仅对内存使用有积极影响，而且对性能也有积极影响。像往常一样，我们进行了一些基准测试来支持这一说法！

基准测试

我们只是简单地使用了与我们发布的所有其他基准测试中使用的相同方法。选择了Arxiv-titles-384-angular-no-filters 和 Gist-960 数据集，以便比较未量化和量化向量。结果总结在下表中：

Arxiv-titles-384-angular-no-filters

搜索精度略有下降，但延迟得到了显著改善。除非您追求最高的精度，否则您应该不会注意到搜索质量上的差异。

Gist-960

在所有情况下，搜索精度的下降都可以忽略不计，但在搜索时，我们仍然保持了至少 28.57% 的延迟降低，甚至高达 60.64%。根据经验法则，向量的维度越高，精度损失越低。

过采样和重评分

Qdrant 架构的一个显著特点是能够在单个查询中结合量化向量和原始向量的搜索。这使得速度、准确性和内存使用达到最佳结合。

Qdrant 存储原始向量，因此在量化空间中进行近邻搜索后，可以使用原始向量对 top-k 结果进行重评分。这显然会对性能产生一定影响，但为了衡量影响程度，我们在不同的搜索场景下进行了比较。我们使用了一台配备非常慢的网络挂载磁盘的机器，并测试了以下允许不同内存量的场景：

以及另一组更严格的内存限制：

在这些实验中，吞吐量主要由磁盘读取次数决定，量化通过允许更多向量驻留在内存中来有效地减少磁盘读取。阅读我们关于 Qdrant 磁盘存储以及如何衡量其性能的文章，了解更多信息：服务百万向量所需的最小内存。

禁用重评分的标量量化机制进一步提升了低端机器的性能极限。如果可以接受搜索精度的小幅下降，处理大量请求似乎不需要昂贵的配置。

访问最佳实践

Qdrant 关于标量量化的文档是一个极好的资源，其中描述了不同的场景和策略，可实现高达 4 倍的内存占用降低，甚至高达 2 倍的性能提升。